计算机图形学.李胜.06.隐藏面的消除
基本概念
- 空间遮挡关系
- 隐藏面/线、可见面/线
- 不同模型
- 表面模型:面消隐
- 线框模型:线消隐
- 深度
- 早期的深度:近大远小
- 现在的深度:近小远大
- 因此在消隐算法中会有初始化以及比大小的不同
消隐的两类方法
- 以像素为循环核心
1 | for(窗口内的每一个像素) { |
- 以物体为循环核心
1 | for(场景中的每一个物体) { |
提高消隐算法效率的常用方法
利用连贯性
- 物体、面、区域、扫描线
将透视投影变换为平行投影
- 消隐与投影方式有关
- 投影中心位置,投影方向
- 平行投影的遮挡关系更好确定
- 现代硬件的实现一般都是 z-buffer
包围盒技术
- 包围盒:包围目标的简单形体
- 常用包围盒:长方体、球、圆柱
- 避免盲目求交
- 如果包围盒不相交,那么物体也一定不会相交
- 包围盒的求交比物体更加简单
- 初级的筛查
常用的包围盒方法
- OBB:面平行
- 紧致的包围盒
- 包围盒的所有面和物体切平面平行
- 可以使用 PCA 的方法找出主轴(3D有3根主轴)
- AABB:轴平齐
- 例如3D,包围盒的所有面都是和轴垂直的简单,不准确
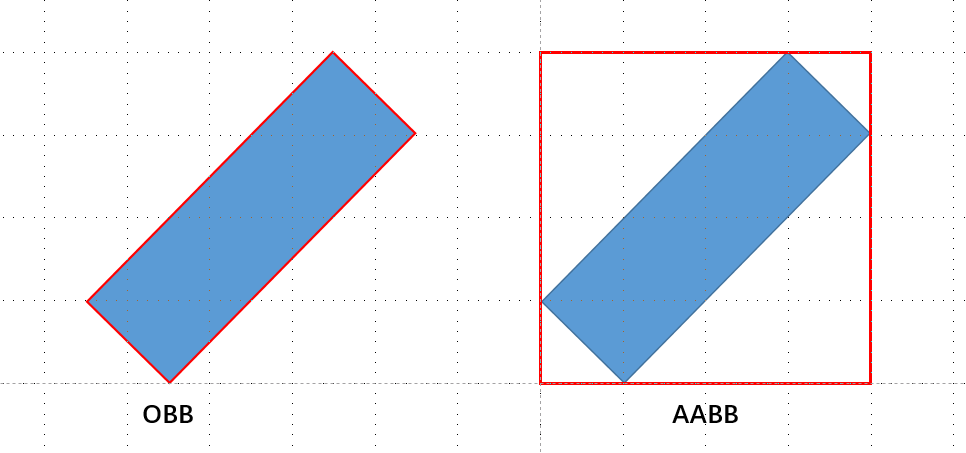
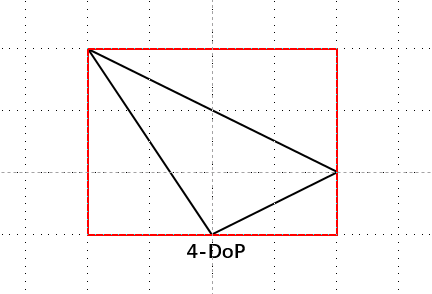
- k-DoP:划分为多个轴,每个轴向找切线
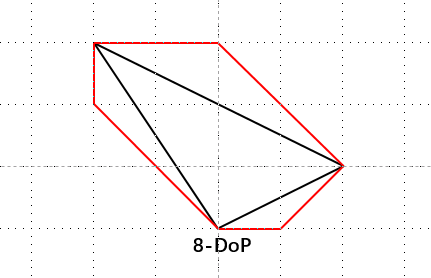
- 层次包围盒
- 树状结构
- 包围盒套包围盒
- 从根出来进行逐个判断,提高效率
背面剔除
- 前向面和后向面(背面)
- 背面是不可见的
- 使用法向判断
- 需要指定 FrontFace
- 顺时针(CW)clockwise
- 逆时针(CCW)counterclockwise
空间分割技术
- 并行渲染
物体的分层表示
- 小汽车
- 车身
- 车头
- 车尾
- 左前轮
- 左后轮
- 右后轮
- 右前轮
- 车身
消隐算法
- 消隐的基本(核心)问题:排序
- 整体排序:画家算法
- 点排序:z-buffer算法、光线投射算法
- 区间排序:扫描线算法
- 区域排序:区域子分算法
画家算法
3D 待绘制的物体进行排序,远处先画,近处后画
- 对场景中的多边形按深度进行排序
- 形成深度优先级表
- 按从远到近的顺序显示多边形
一维空间(数轴)上点的排序
二维平面上直线段的排序
- 两条直线段可能相交
- 分类讨论,包围盒
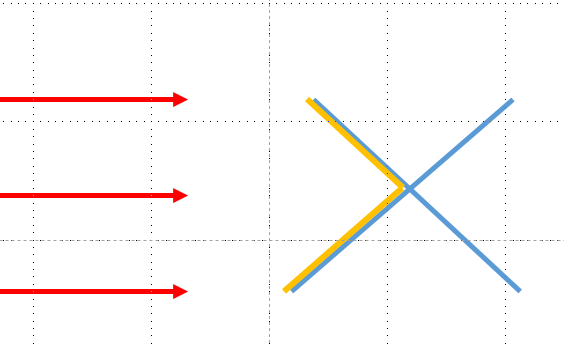
- 两条直线段可能相交
三维空间中多边形的排序
- 连环套问题
- 解套:拆分单个面片

- 连环套问题
z-buffer 算法
- 窗口与缓冲器
- 绘图窗口
- 帧缓冲器:存放对应像素的颜色
- z(深度)缓冲器:存放对应像素的深度值
- z 缓冲器算法
- 初始化所有像素深度值为 1(最大深度),颜色值为背景色
- 对多边形的投影区域的每一个像素循环
- 逐像素比较深度,若小于 z-buffer 中存的深度,则更新两个缓冲器
- 优点
- 算法简单、稳定
- 便于硬件加速
- 不需要整个场景的几何数据
- 缺点
- 需要 z 缓冲器
- 计算复杂度大
- 需要计算的像素深度值次数 = 多边形个数*多边形平均占据的像素个数
扫描线 z-buffer 算法
经典但是过时的算法
早期在 z-buffer 数量不够时提出的算法
需要的 z-buffer 数目从原来的整个窗口减少到一条扫描线
- 随着技术发展,z-buffer 已经不再是稀缺资源,可以支持整个窗口,因此现在很少用
扫描线 z-buffer 算法
- 将窗口划分为多条扫描线
- 初始化扫描线对应的两个缓冲器
- 对每个多边形循环
- 求出每个多边形的投影区域与扫描线的的相交区间
- 比较深度与对应像素在 z-buffer 中的深度值,看是否需要更新两个缓冲器
- 将窗口划分为多条扫描线
复杂度高
- 每一条扫描线都需要和多边形进行相交测试
- 需要计算相交区间的深度值
数据结构
(1) 多边形顶点数组
- 二维数组 \(P[i][j]\),元素是三维坐标
- 第 i 个多边形的第 j 个顶点
(2) 多边形
- 平面信息:a,b,c,d
- 多边形所在平面:\(f(u,v,n)=au+bv+cn+d=0\)
- 多边形颜色值:color
- 投影的最大 v 坐标:\(v_{max}\)
- 多边形的序号:PI
- 指向下一个多边形结构的指针:nextP
(3) 多边形分类表 PT
- 一维数组,长度等于绘图窗口内扫描线的数目,元素为多边形
- 如果一个多边形的投影的最小 v 坐标为 v,那么它就属于 v 类
(4) 活化多边形表 APL
- 记录投影与当前扫描线相交的多边形
- 多边形在 APL 中的顺序无关紧要
(5) 边
- 用于记录多边形的一条边
- 边结构
- 边投影上端点的 v 坐标:\(v_{max}\)
- 边投影下端点的 u 坐标:u
- 边投影下端点的 n 坐标:n
- 在该边上 v 值增加一个单位时,u 坐标的变化量:\(\Delta u\)
- 指向下一个边结构的指针:nextE
(6) 边分类表 ET
- 当一个多边形进入活化多边形表的时候,需要为其建立一个边分类表
- 不处理的就不需要建立了
- 对非水平边进行分类的一维数组
- 一维数组,长度等于扫描线的数目,元素为边
- 若一条边的下端点的 v 坐标为 v,则将该边归为第 v 类
(7) 边对
- 在一条扫描线上,同一多边形的相邻两条边称为边对
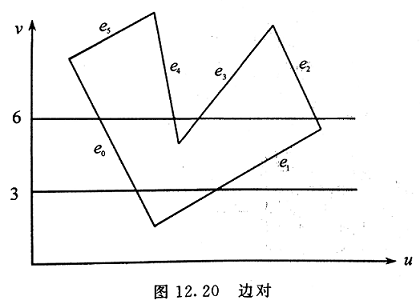
- 扫描线 3 对应的边对:\(e_0e_1\)
- 扫描线 6 对应的边对:\(e_0e_4,e_3e_2\)
- 边对中包含了大量信息,是该消隐算法的核心单元
边对包含信息
- \(u_l\):边对左侧边与扫描线交点的 u 坐标
- \(\Delta u_l\):当沿左侧边 v 坐标递增一个像素时,u 坐标的增量
- \(v_{lmax}\):左侧边投影的上端点的 v 坐标
- \(u_r,\Delta u_r,v_{rmax}\)
- \(n_l\):左侧边与扫描线的交点处的多边形的 n 坐标(深度)
- \(\Delta n_u\):当沿着扫描线 u
递增一个像素时,多边形所在平面的 n 坐标的增量
- \(f(u,v,n)=au+bv+cn+d=0\Rightarrow\Delta n_u=\dfrac{-a}{c}(c\ne0)\)
- \(\Delta n_v=\dfrac{-b}{c}(c\ne0)\)
- PI:多边形序号
- nextEP:指向下一个边对结构的指针,用于将边连接成链表
(8) 活化边对表 AEPL
- 记录了活化多边形表中与当前扫描线相交的边对(顺序无关紧要)
算法
建立多边形分类表 PT
置活化多边形表 APL 为空,置活化边对表为空
对每条扫描线执行以下操作
- 置帧缓冲器第 v 行的各单元为背景色
- 置 z 缓冲器个单元的值为 1(最大的深度值)
- 检查 PT 的第 v 类是否非空,如果非空,则将该类的多边形去除加入到 APL 中
- 对新加入 APL 的每个多边形,为其建立边分类表 ET
- 对新加入 APL 的每个多边形,若他的 ET 中第 v 类非空,将其中的边对出插入 APEL 中
- 对 APEL 中的每一个边对,执行以下步骤
\[ \begin{aligned} &深度值 n=n_l\\ &for(u = u_l; u <= u_r; u = u + 1) \{\\ &\qquad if(n < z 缓冲器中第 u 个单元的深度值) \{\\ &\qquad\qquad 置帧缓冲器第 (u,v) 单元的值为当前便对所属的多边形的颜色;\\ &\qquad\qquad 置 z 缓冲器第 u 单元的值为 n;\\ &\qquad\}\\ &\qquad n = n + \Delta n_u; // 计算下一个像素 (u + 1,v) 处的深度值\\ &\}\\ \end{aligned} \]
- 检查 APL,删除那些满足 \(v=v_{max}\) 的多边形,释放该多边形的 ET,并从 AEPL 中删除属于该多边形的边对
- 检查 AEPL 中的边对,执行以下步骤
- 若 \(v_{lmax}=v\) 或者 \(v_{rmax}=v\) ,删除边对的左侧边或者右侧边
- 若边对的左侧边和右侧边都被删除了,则从 AEPL 中将这个边对删去
- 若边对只被删去一条边,那么从其所属的多边形找另一条边和其配对成为新的边对,加入 APEL
- 若 \(v_{lmax}=v\) 或者 \(v_{rmax}=v\) ,删除边对的左侧边或者右侧边
- 将扫描线向下移动一个像素 v = v + 1
算法说明
- 一定配对
- 一条直线和封闭多边形相交的边数为偶数(不计直线和多边形顶点的相交)
- 删除 AEPL 中的边对
- 扫描线从下向上移动
- 删除时整个边对之间的区域都被上色了
评价
- 和 z 缓冲器相比改进的地方
- 将窗口分割成扫描线,只需要一条扫描线的 z-buffer
- 采用多边形分类表、活化多边形表避免多边形与扫描线的盲目求交
- 利用边、边的分类表、边对、活化边对表避免边与扫描线的盲目求交
- 利用连贯性计算深度
- 缺点
- 在每一个被多边形覆盖像素处需要计算深度值
- 被多个多边形覆盖的像素需要多次计算深度值
扫描线算法
相较于 z-buffer 扫描线算法的改进
- 在一条扫描线上,以区间为单位确定多边形的可见性
- 在一条扫描线上,每个区间只需要计算一次深度值
- 不需要 z-buffer
- 在一条扫描线上,以区间为单位确定多边形的可见性
算法思想
- 两个多边形(记作 \(P_1,P_2\)) 的边界将扫描线分割为多个区间
- 覆盖每段区间的多边形可能有 0 个或者多个,但是只有一个可见
- 因此对于每段区间,我们只需要任取一个点,计算深度,找到深度最小的点,用它所在多边形的颜色为当前像素点上色即可(帧缓冲器)
算法局限
- 要求多边形不能相互贯穿
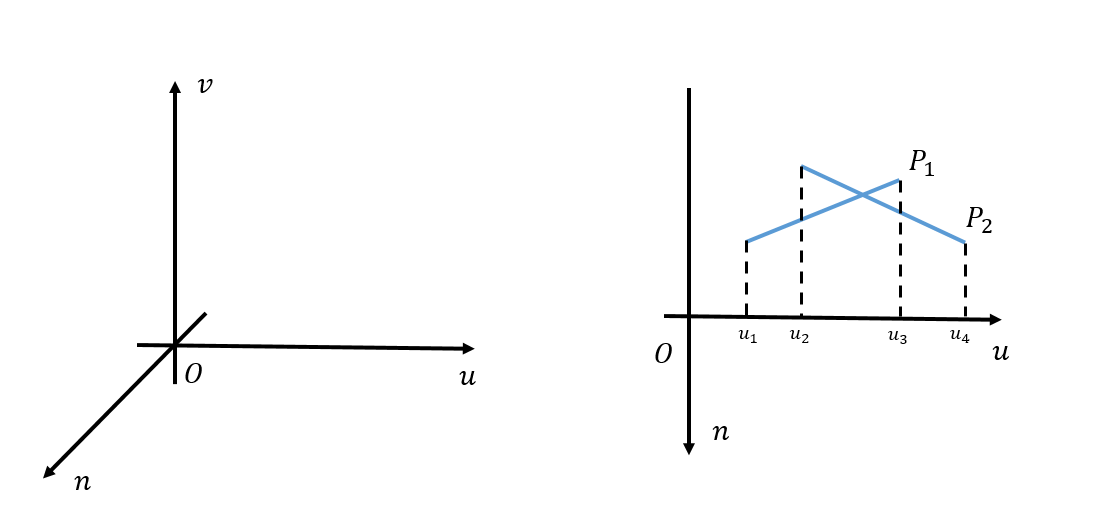
- 否则需要计算多边形相交的点作分界(让算法复杂度变高)
- 如上图
- 区间 \([0,u_1],[u_1,u_2],[u_2,u_3],[u_3,u_4],[u_4,u_{max}]\)
- 出现贯穿的情况,在区间 \(,[u_2,u_3]\) 中出现深度变化
区域子分算法
- 不把像素孤立起来看待,考虑区域连贯性
- 扫描线算法中的区间本质也是一种对于区域连贯性的考虑
- 利用区域的连贯性提高排序的效率
- 分割窗口直到窗口足够简单
- 窗口足够简单:满足以下几种条件之一即可
- 窗口为空:所有多边形和当前窗口的关系都是分离
- 窗口内仅包含一个多边形:仅有一个多边形与当前窗口相交或者包含于当前窗口
- 窗口被一个多边形包围,并且它是离视点最近的
- 四叉树
光线投射算法
- 基本问题:光线与物体表面求交
1 | for(v = 0; v <= vmax; v++) { |
- 特殊情况
- 光线穿越物体的边缘 / 顶点
- 需要自己定义 visible / invisible
(半)透明问题
- z-buffer test:用于确定物体的深度关系
- 如果物体透明怎么办?
- 顺序?
- 需要考虑混合顺序:排序
- 去除透明物体,融合半透明物体与最近的不透明物体
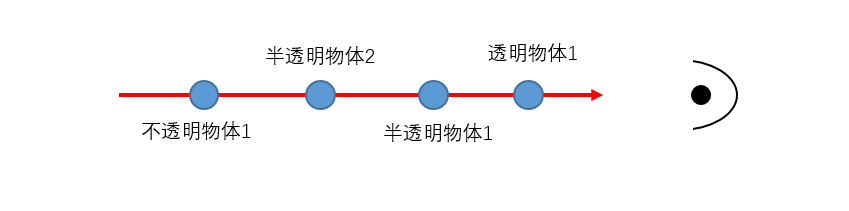
- 排序
- order dependent transparency:物体级别的排序
- 显式对物体进行排序
- order independent transparency:片元级别的排序
- order dependent transparency:物体级别的排序
A-buffer 算法
- order dependent transparency
- 对于每个像素,形成一个链表结构
- 链表内按照深度排序,之后可以通过类似于之前的方式进行上色
Depth Peeling 深度剥离
- order independent transparency
- 多次渲染
- 每次渲染去除之前已经渲染的片元,把剩下的片元都当作不透明的处理
- 相当于每次渲染得到深度最小的片元结果,将其存到一个 buffer 里面
- 最后融合这些 buffer
- 浪费了大量片元,大量空间都是空白的
半透明顺序
- 如提前知道半透明的顺序,直接排序即可
- 如果不知道,可以使用 A-buffer 或者 Depth Peeling 等算法
Dual Depth Peeling 双向深度剥离
- 渲染次数减半
光线跟踪
- 非传统渲染管线
- 直接考虑了半透明的信息