计算机图形学.李胜.05.投影(2)
OpenGL 中的投影矩阵
- vmath:Frusutm()
\[ \begin{bmatrix} \dfrac{2near}{right-left}&0&A&0\\ 0&\dfrac{2near}{top-bottom}&B&0\\ 0&0&C&D\\ 0&0&-1&0\\ \end{bmatrix} \]
- 其中 \(A,B,C,D\) 含义如下
\[ A=\dfrac{left+right}{right-left} \]
\[ B=\dfrac{top+bottom}{top-bottom} \]
\[ C=-\dfrac{far+near}{far-near} \]
\[ D=-\dfrac{2far\cdot near}{far-near} \]
- 其中 \(far,near,top,bottom,left,right\)
表示6个裁剪面
- 实际的裁剪面
- \(far,near\) 使用的是绝对值
- 因为一定是负数
- \({\color{red}-far,-near},top,bottom,left,right\)
- \(far,near\) 使用的是绝对值
- 实际的裁剪面
- 坐标变换:
- 现实坐标系中的视见体 转化为 OpenGL中的立方体 \([-1,1]\)
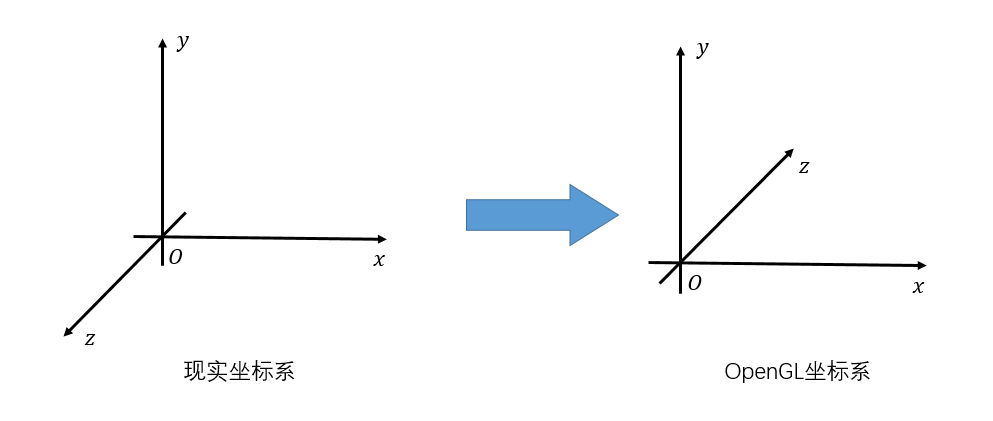
- 投影中心 \((0,0,0)\)
- 投影平面 \(z=-near\)
- 推导过程中裁剪面使用单词首字母代替
推导一:投影角度
- 投影+规范化
(1) 投影
- 将视见体中的点投影到 \(z=-n\) 上
- 以俯视图为例推导坐标关系(\(x,z\))
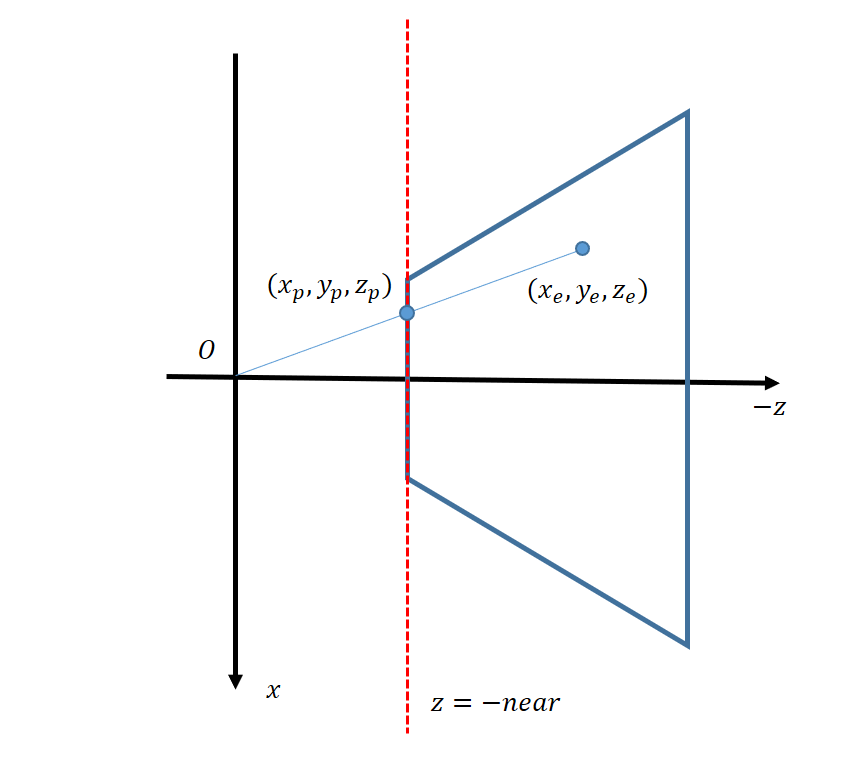
- \(z_p=-n\)
- \(x_p=\dfrac{nx_e}{-z_e}\)
- 利用侧视图可以得到 \(y_p=\dfrac{ny_e}{-z_e}\)
(2) 规范化
\(x_p\in[l,r]\rightarrow x_n\in[-1,1]\)
\(y_p\in[b,t]\rightarrow y_n\in[-1,1]\)
以 \(x\) 的推导为例
- \(\dfrac{x_p-l}{r-l}=\dfrac{x_n-(-1)}{1-(-1)}\)
- \(x_n=2\dfrac{x_p-l}{r-l}-1=\dfrac{2}{r-l}x_p-\dfrac{r+l}{r-l}=\dfrac{2n}{-z_e(r-l)}x_e-\dfrac{r+l}{r-l}\)
- \(x_n=\dfrac{\dfrac{2n}{r-l}x_e+\dfrac{z_e(r+l)}{r-l}}{-z_e}\)
同理
- \(y_n=\dfrac{\dfrac{2n}{t-b}y_e+\dfrac{z_e(t+b)}{t-b}}{-z_e}\)
写成矩阵的形式
为了计算的方便,我们把分母放到最终的齐次坐标化简中去
\(w_c=-z_e,x_n=\dfrac{x_c}{w_c},y_n=\dfrac{y_c}{w_c}\)
\[ \begin{bmatrix} \dfrac{2n}{r-l}&0&\dfrac{r+l}{r-l}&0\\ 0&\dfrac{2n}{t-b}&\dfrac{t+b}{t-b}&0\\ \cdot&\cdot&\cdot&\cdot\\ 0&0&-1&0 \end{bmatrix} \begin{bmatrix} x_e\\y_e\\z_e\\w_e \end{bmatrix} = \begin{bmatrix} x_c\\y_c\\z_c\\w_c \end{bmatrix} \]
(3) 记录深度信息
\[ \begin{bmatrix} \dfrac{2n}{r-l}&0&\dfrac{r+l}{r-l}&0\\ 0&\dfrac{2n}{t-b}&\dfrac{t+b}{t-b}&0\\ 0&0&A&B\\ 0&0&-1&0 \end{bmatrix} \begin{bmatrix} x_e\\y_e\\z_e\\w_e \end{bmatrix} = \begin{bmatrix} x_c\\y_c\\z_c\\w_c \end{bmatrix} \]
我们可以看到, \(z_n\) 并没有被用上,我们可以用来记录深度信息
\(z_n=\dfrac{z_c}{w_c}=\dfrac{Az_e+Bw_e}{w_c}=\dfrac{Az_e+B}{-z_e}=-A+\dfrac{B}{-z_e}\)
\(z_e\in[{\color{red}-f},-n]\rightarrow z_n\in[{\color{red}1},-1]\)
- 深度值越远越大
\[ \left\{ \begin{array}{**lr**} 1=-A+\dfrac{B}{f}\\ -1=-A+\dfrac{B}{n} \end{array} \right. \Rightarrow \left\{ \begin{array}{**lr**} A=-\dfrac{f+n}{f-n}\\ B=-\dfrac{2nf}{f-n} \end{array} \right. \]
推导二:变换角度
- 错切+缩放+规范化
(1) 错切
- 错切至关于 z 轴中心对称
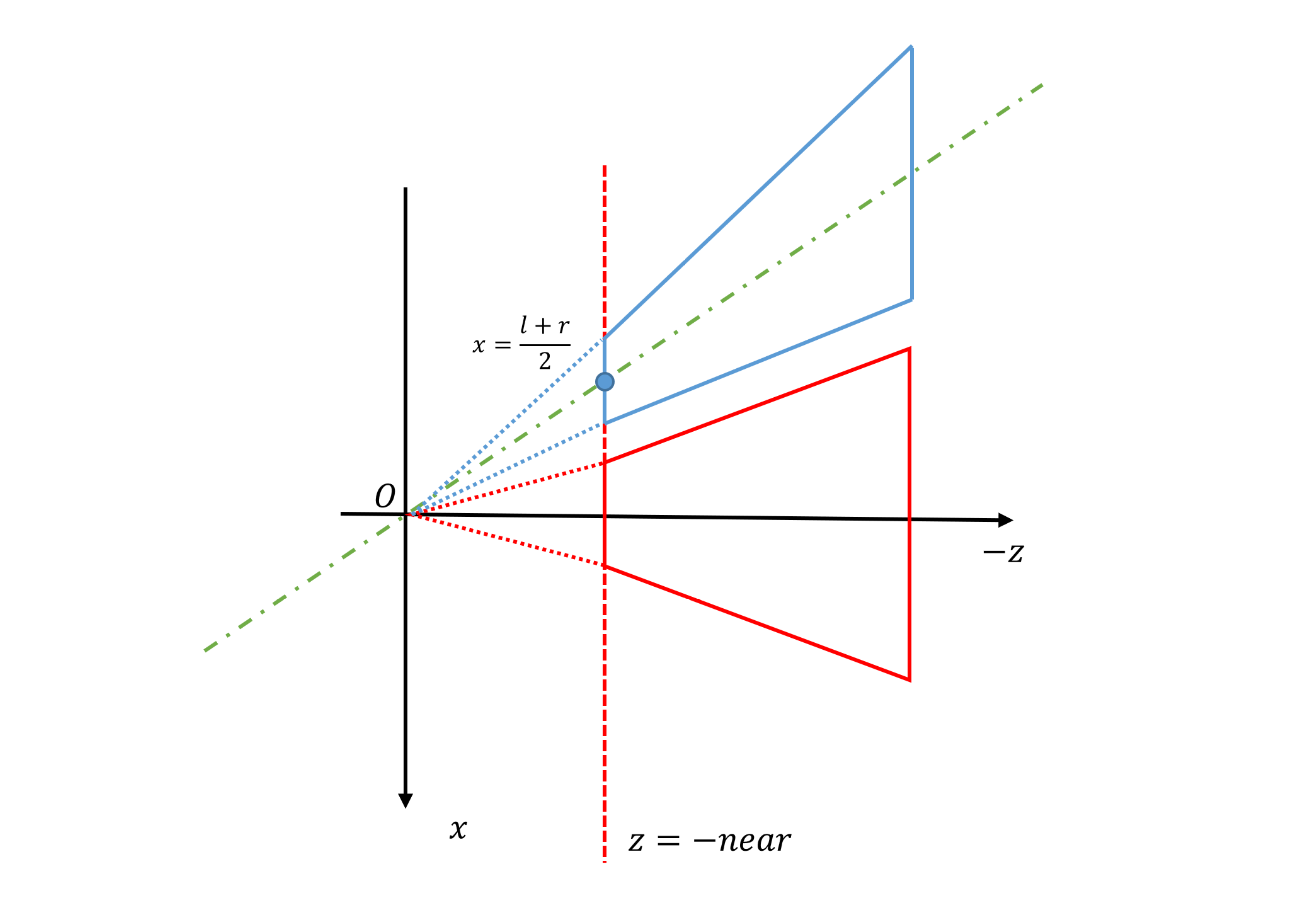
- \(-x\) 方向:\(\tan\theta_x=\dfrac{1}{2}\cdot\dfrac{l+r}{-n}\)
- \(\Rightarrow +x:\tan\theta_x'=\dfrac{l+r}{2n}\)
- \(-y\) 方向:\(\tan\theta_y=\dfrac{1}{2}\cdot\dfrac{t+b}{-n}\)
- \(\Rightarrow +y:\tan\theta_y'=\dfrac{t+b}{2n}\)
\[ M_1= \begin{bmatrix} 1&0&\dfrac{l+r}{2n}&0\\ 0&1&\dfrac{t+b}{2n}&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} \]
(2) 缩放
- 缩放的结果
- \(x:[l,r]\to[-1,1]\)
- \(y:[b,t]\to[-1,1]\)
- \(z:[{\color{red}-f},-n]\to
[{\color{red}-1},-\dfrac{f}{n}]\)
- 因此,对应着投影平面 \(z=-1\) 的是后裁剪面 \(z=-f\)
\[ M_2= \begin{bmatrix} \dfrac{2n}{(r-l)f}&0&0&0\\ 0&\dfrac{2n}{(t-b)f}&0&0\\ 0&0&\dfrac{1}{f}&0\\ 0&0&0&1 \end{bmatrix} \]
- 等价于 \(M_2'\)(化成标准齐次坐标是一样的)
\[ M_2'= \begin{bmatrix} \dfrac{2n}{r-l)f}&0&0&0\\ 0&\dfrac{2n}{t-b}&0&0\\ 0&0&1&0\\ 0&0&0&f \end{bmatrix} \]
- 以上形成的视见体其实是一个棱台
- 顶点为 \((0,0,0)\) 底面为 \((-1,-1,0),(-1,1,0),(1,1,0),(1,-1,0)\) 的四棱锥被平面 \(z=-\dfrac{n}{f}\) 截成的四棱锥
(3) 透视=>平行
- 将透视投影的规范视见体变换为平行投影的规范视见体
- 将上述四棱锥转换为长方体
- \(x:[-1,1]\to[-1,1]\)
- \(y:[-1,1]\to[-1,1]\)
- \(z:[{\color{red}-1},-\dfrac{f}{n}]\to [-1,0]\)
\[ M_3= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&\dfrac{1}{1-n_{min}}&\dfrac{n_{min}}{1-n_{min}}\\ 0&0&-1&0 \end{bmatrix} \]
- \(z_{min}\ge0\)
\[ M_3= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&\dfrac{f}{f-n}&\dfrac{n}{f-n}\\ 0&0&-1&0 \end{bmatrix} \]
- 推导过程和 推导一的投影 相似
- \(\dfrac{x_p}{z_p}=\dfrac{x_n}{-1},\dfrac{y_p}{z_p}=\dfrac{y_n}{-1}\)
- \(x_n=\dfrac{x_p}{-z_p},y_n=\dfrac{y_p}{-z_p}\)
- 得到矩阵如下
\[ M_3= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ \cdot&\cdot&\cdot&\cdot\\ 0&0&-1&0 \end{bmatrix} \]
- 将第三行用于记录深度信息
\[ M_3= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&A&B\\ 0&0&-1&0 \end{bmatrix} \]
\(z_n=\dfrac{Az_p+B}{-z_p}=-A+\dfrac{B}{-z_p}\)
- \[ \left\{ \begin{array}{**lr**} -1=-A+\dfrac{B}{1}\\ 0=-A+\dfrac{B}{n_{min}} \end{array} \right. \Rightarrow \left\{ \begin{array}{**lr**} A=\dfrac{1}{1-n_{min}}\\ B=\dfrac{n_{min}}{1-n_{min}} \end{array} \right. \]
(4) 平移
- \(x:[-1,-1]\to[-1,1]\)
- \(y:[-1,-1]\to[-1,1]\)
- \(z:[-1,0]\to -[\dfrac{1}{2},\dfrac{1}{2}]\)
\[ M_4= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&\dfrac{1}{2}\\ 0&0&0&1 \end{bmatrix} \]
(5) 尺缩
- \(x:[-1,-1]\to[-1,1]\)
- \(y:[-1,-1]\to[-1,1]\)
- \(z:[-\dfrac{1}{2},\dfrac{1}{2}]\to [-1,1]\)
\[ M_5= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&2&0\\ 0&0&0&1 \end{bmatrix} \]
(6) 深度变换
- 深度越大 \(z\) 越大
\[ M_6= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\ 0&0&0&1 \end{bmatrix} \]
(7) 结果
- 与上面一致
\[ M_6M_5M_4M_3M_2'M_1 \]