计算机图形学.李胜.05.投影(1)
三维图形的基本问题
- 在二维屏幕上显示三维物体
- 投影
- 三维形体的表示
- 各种用于形体表示的理论、模型、方法
- 反映遮挡关系
- 消除隐藏面与隐藏线
- 产生真实感图形
- 建立光照明模型、开发真实感图形绘制方法
平面几何投影
- 投影
- 将 n 维的店变换成小于 n 维的点
- 3 => 2
- 投影中心
- COP:Center Of Projection
- 视觉系统:观察点、视点
- 电影放映机:光源
- 投影平面
- 又称为观察平面 VP(View Plane)
- 不经过投影中心
- 平面(照相机底片),曲面(球幕电影、视网膜)
- 投影线
- 从投影中心向物体上各点发出的射线
- 直线:光线
- 曲线:光线跟踪
- 平面几何投影
- 投影面为平面
- 投影线为直线
- 包括透视投影和平行投影
- 透视投影:投影中心与投影平面之间的距离有限
- 平行投影:投影中心与投影平面之间的距离无限
- 透视投影
- 灭点:不平行于投影平面的平行线,经过透视投影之后收敛于一点,称为灭点
- 主灭点:平行于坐标轴的平行线的灭点
- 按照主灭点个数分类
- 一点透视:投影平面平行于 xOy 平面
- 两点透视:投影平面平行于 y 轴,与 x、z 轴都有交点
- 三点透视:投影平面与 x、y、z 轴都有交点
- 产生近大远小的视觉效果,由它产生的图形深度感强,看起来更加真实
- 《最后的晚餐》:只有一个主灭点,耶稣的头部
- 平行投影
- 正投影与斜投影
- 正投影:投影方向垂直于投影平面
- 斜投影:投影方向不垂直投影平面
- 三视图
- 正视图、侧视图、俯视图
- 不能无误的重现原模型
观察坐标系中的投影变换
观察坐标系:
- VRC:View Reference Coordinate
- 照相机所在坐标系
建立观察坐标系
坐标原点:VRP(View Reference Point)
- 聚焦参考点与投影平面上的投影
n 轴
- 照相机的镜头方向(投影平面的法向)
v 轴
- 照相机向上的方向(观察正向 VUP 在投影平面的投影)
u 轴
\(u=v\times n\)
叉乘转化为矩阵
\(\vec{a}\times\vec{b}=(a_2b_3-b_2a_3,a_3b_1-b_3a_1,a_1b_2-b_1a_2)\)
- \((a_1\vec{i}+a_2\vec{j}+a_3\vec{k})\times(b_1\vec{i}+b_2\vec{j}+b_3\vec{k})\) 展开即可
\[ \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} \]
\((u,v,n)\)
投影平面:\(n=0\)
投影中心:\((0,0,d)\)
视见体:三维裁剪窗口
- 6 个裁剪面
投影参考点:PRP(Projection Reference Point)
- 透视投影:COP = PRP
- 平行投影:投影方向(DOP)= 窗口中心 CW 和 PRP 的连线
投影参数表
| 参数 | 作用 |
|---|---|
| 投影类型 | 定义投影是平行投影还是透视投影 |
| 观察参考点 \(VRP\) | 在世界坐标系中指定,为观察坐标系原点 |
| 观察平面法向 \(VPN\) | 在世界坐标系中指定,为观察坐标的 \(n\) 轴 |
| 观察正向 \(VUP\) | 在世界坐标系中指定,确定观察坐标系的 \(v\) 轴 |
| 投影参考点 \(PRP\) | 在观察坐标系中指定确定投影中心或投影方向 |
| 前裁剪面裁距 \(F\) | 在观察坐标系中指定,\(n=F\) 为前裁剪面 |
| 后裁剪面裁距 \(B\) | 在观察坐标系中指定,\(n=B\) 为后裁剪面 |
| 窗口 \(u_{min},u_{max},v_{min},v_{max}\) | 在观察坐标系的uv平面上指定,确定窗口与视见体 |
- 窗口不一定关于原点对称
三维空间直线参数方程
- 过顶点 \(A(x_0,y_0,z_0)\),方向向量 \((m,n,p)\),直线参数方程如下
\[ \left\{ \begin{array}{**lr**} x=t(m-x_0)+x_0\\ y=t(n-y_0)+y_0\\ z=t(p-z_0)+z_0 \end{array} \right.or \left\{ \begin{array}{**lr**} x=tm+x_0\\ y=tn+y_0\\ z=tp+z_0 \end{array} \right. \]
透视投影变换求解
投影中心\((0,0,d)\),待投影点 \(P(u_p,v_p,n_p)\),求解在投影平面 \(n=0\) 的投影点 \(Q(u_q,v_q,n_q)\)
投影线的参数方程(经过投影中心\((0,0,d)\)) \[ \left\{ \begin{array}{**lr**} u=tu_p & \\ v=tv_p & t\ge 0\\ n=t(n_p-d)+d & \end{array} \right. \]
求解,令 \(n=0\)
\[ \left\{ \begin{array}{**lr**} u_q=\dfrac{u_p}{1-\dfrac{n_p}{d}} \\ v_q=\dfrac{v_p}{1-\dfrac{n_p}{d}} \\ n_q=0 \end{array} \right. \]
- 将其写作矩阵形式 \(Q=M_{per}P\)
- 注意得到的结果需要进行标准化 \(h\ne 1\)
\[ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & -\dfrac{1}{d} &1\\ \end{bmatrix} \]
平行投影变换求解
- 投影平面 \(n=0\),投影方向 \((0,0,-1)\),待投影点为 \(P(u_p,v_p,n_p)\),求投影点 \(Q(u_q,v_q,n_q)\)
- \(Q(u_p,v_p,0)\)
- 将其写作矩阵形式 \(Q=M_{ori}P\)
\[ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]
- \(\lim_\limits{d\to\infty}M_{per}=M_{ori}\)
世界坐标系WC到观察坐标系VRC的变换
- 条件
- WC:xyz,VRC:uvn
- VRC 的坐标原点 VRP \((VRP_x,VRP_y,VRP_z)\)
- 投影平面法向 \(\vec{VPN}\)
- 观察正向 \(\vec{VUP}\)
- 做如下记号
\[ \left\{ \begin{array}{**lr**} \vec{n}=\dfrac{\vec{VPN}}{|\vec{VPN}|}=[n_x,n_y,n_z]\\ \vec{u}=\dfrac{\vec{VUP}\times\vec{VPN}}{|\vec{VUP}\times\vec{VPN}|}=[u_x,u_y,u_z] \\ \vec{v}=\vec{n}\times\vec{u} \end{array} \right. \]
- 先平移后旋转
\[ M_{WC\to VRC}= \begin{bmatrix} u_x & u_y & u_z & 0\\ v_x & v_y & v_z & 0\\ n_x & n_y & n_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -VRP_x\\ 0 & 1 & 0 & -VRP_y\\ 0 & 0 & 1 & -VRP_z\\ 0 & 0 & 0 & 1\\ \end{bmatrix} =RT \]
证明1:直接通过线性代数的知识,两个空间的正交变换为 \(R\)
- 直接验证结果也是显然正确的
证明2:参考《计算机图形学 倪眀田 吴良芝》P143-145
平移变换显然,我们只考虑两个坐标系的原点相同旋转部分
通过解构的方法证明
步骤如下
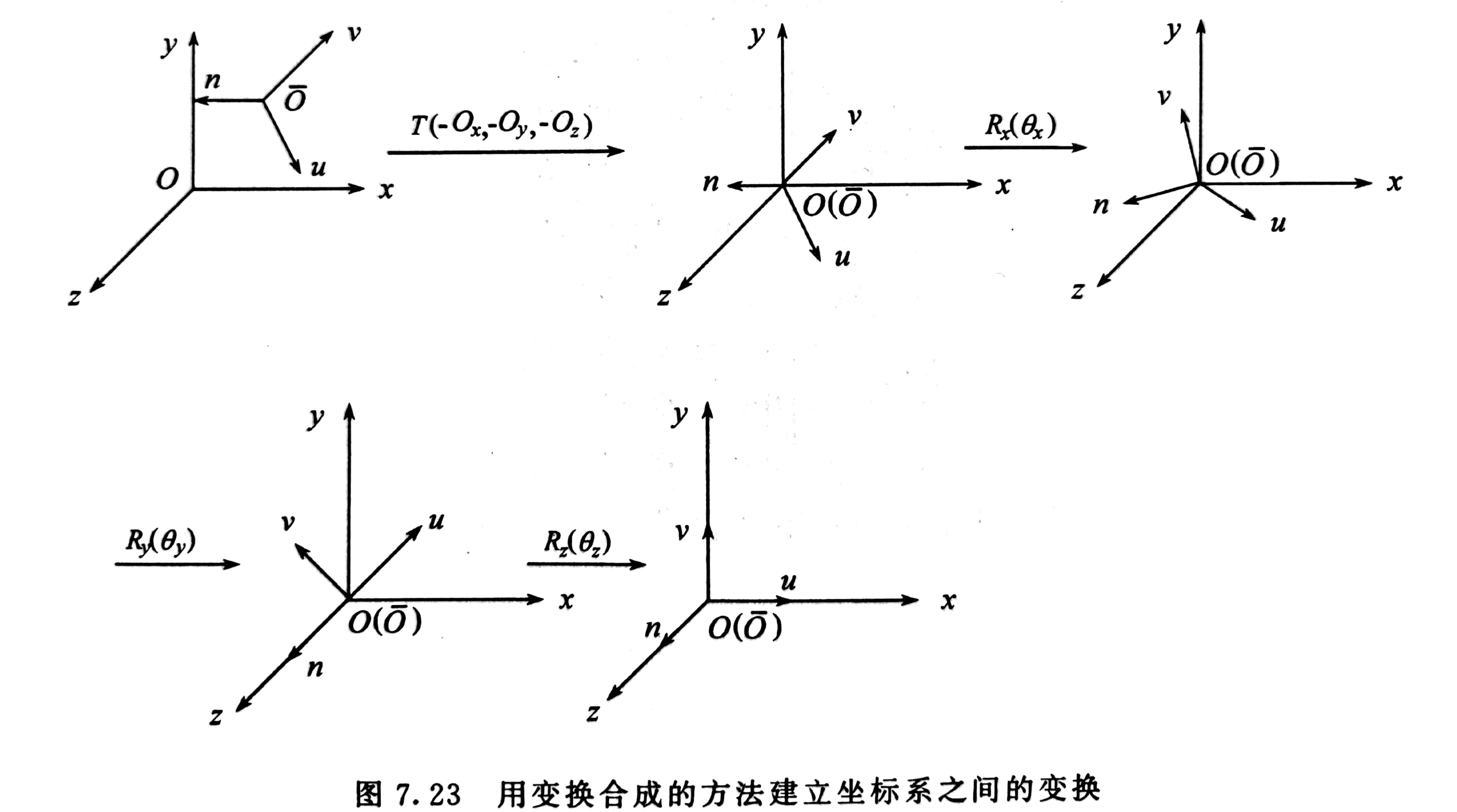
绕 x 轴旋转角度 \(\theta_x\) 使得 n 轴落于 xOz 平面 \[ \cos\theta_x=\dfrac{n_z}{\sqrt{n_y^2+n_z^2}},\qquad \sin\theta_x=\dfrac{n_y}{\sqrt{n_y^2+n_z^2}} \]
绕 y 轴旋转角度 \(\theta_y\) 使得 n 轴和 z 轴同向且重合 \[ \cos\theta_y=\sqrt{n_y^2+n_z^2},\qquad \sin\theta_y=n_x \]
绕 z 轴旋转角度 \(\theta_z\) 使得 u 轴和 x 轴同向且重合
这一部分比较麻烦,可以先用上面的变换得到在世界坐标系中单位向量对应的点 \(\vec{u}\) 的位置
注意有
- \(\vec{u}\cdot\vec{n}=u_xn_x+u_yn_y+u_zn_z=0\)
- \(\vec{n}\times\vec{u}=(n_yu_z-u_yn_z,n_zu_x-u_zn_x,n_xu_y-u_xn_y)=(v_x,v_y,v_z)\)
\[ R_y(\theta_y)= \begin{bmatrix} \sqrt{n_y^2+n_z^2} & 0 & -n_x & 0\\ 0 & 1 & 0 & 0\\ n_x & 0 & \sqrt{n_y^2+n_z^2} & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\\ \]
\[ R_x(\theta_x)= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \dfrac{n_z}{\sqrt{n_y^2+n_z^2}} & -\dfrac{n_y}{\sqrt{n_y^2+n_z^2}} & 0\\ 0 & \dfrac{n_y}{\sqrt{n_y^2+n_z^2}} & \dfrac{n_z}{\sqrt{n_y^2+n_z^2}} & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\\ \]
\[ R_y(\theta_y)R_x(\theta_x)= \begin{bmatrix} \sqrt{n_y^2+n_z^2} & -\dfrac{n_xn_y}{\sqrt{n_y^2+n_z^2}} & -\dfrac{n_xn_z}{\sqrt{n_y^2+n_z^2}} & 0\\ 0 & \dfrac{n_z}{\sqrt{n_y^2+n_z^2}} & -\dfrac{n_y}{\sqrt{n_y^2+n_z^2}} & 0\\ n_x & n_y & n_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]
\[ \vec{u}=R_y(\theta_y)R_x(\theta_x)\begin{bmatrix} u_x\\ u_y\\ u_z\\ 1 \end{bmatrix} = \begin{bmatrix} \dfrac{u_x}{\sqrt{n_y^2+n_z^2}}\\ \dfrac{u_yn_z-u_zn_y}{\sqrt{n_y^2+n_z^2}}\\ 0\\ 1\\ \end{bmatrix} \]
此时的 \(|\vec{u}|=1\),旋转不改变长度
- 那么同时就会有 \(u_x^2+v_x^2+n_x^2=1\)
或者直接计算
\[ \begin{aligned} &u_x^2+(u_yn_z-u_zn_y)^2 \\ =\ &u_x^2+v_x^2\\ & u_x^2+(u_yn_z-u_zn_y)^2 \\ =\ &u_x^2+u_y^2n_z^2+u_z^2n_y^2-2n_yu_yn_zu_z\\ =\ &u_x^2+u_y^2(1-n_x^2-n_y^2)+u_z^2(1-n_x^2-n_z^2)-2n_yu_yn_zu_z\\ =\ &1-u_y^2n_x^2-u_y^2n_y^2-u_z^2n_x^2-u_z^2n_z^2-2n_yu_yn_zu_z\\ =\ &1-u_y^2n_x^2-u_z^2n_x^2-(u_yn_y+u_zn_z)^2\\ =\ &1-u_y^2n_x^2-u_z^2n_x^2-(u_xn_x)^2\\ =\ &1-n_x^2\\ \end{aligned} \]
\(\Rightarrow u_x^2+v_x^2+n_x^2=1\)
此时可以推导出 \(\theta_z\)
\[ \cos(-\theta_z)=\dfrac{u_x}{\sqrt{n_y^2+n_z^2}} \]
\[ \sin(-\theta_z)=\dfrac{u_yn_z-u_zn_y}{\sqrt{n_y^2+n_z^2}} \]
\[ \cos(\theta_z)=\dfrac{u_x}{\sqrt{n_y^2+n_z^2}}=\dfrac{v_yn_z-n_yv_z}{\sqrt{n_y^2+n_z^2}} \]
\[ \sin(\theta_z)=-\dfrac{u_yn_z-u_zn_y}{\sqrt{n_y^2+n_z^2}}=\dfrac{v_x}{\sqrt{n_y^2+n_z^2}} \]
乘法时根据次数把 \(\sin\theta_x,\cos\theta_z\) 展开为不同形式 \[ R_z(\theta_z)= \begin{bmatrix} \cos\theta_z & -\sin\theta_z & 0 & 0\\ \sin\theta_z & \cos\theta_z & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}\\ \]
\[ R_z(\theta_z)R_y(\theta_y)R_x(\theta_x)= \begin{bmatrix} u_x & u_y & u_z & 0\\ v_x & v_y & v_z & 0\\ n_x & n_y & n_z & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]