计算机图形学.李胜.04.几何变换
二维基本变换
1. 平移变换
- \(\vec{P'}=\vec{P}+\vec{T}\)
\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix}+\begin{bmatrix}t_x \\ t_y\end{bmatrix} \]
2. 旋转变换
- \(\vec{P'}=R_{\theta}\cdot\vec{P}\)
\[ R_{\theta}=\begin{bmatrix}\cos \theta & -\sin\theta \\ \sin\theta&\cos\theta\end{bmatrix} \]
- \(R_{\theta}=R_{-\theta}^{-1}\)
3. 尺度变换
- \(\vec{P'}=S\cdot\vec{P}\)
\[ S=\begin{bmatrix}s_x & 0 \\ 0 & s_y \end{bmatrix} \]
齐次坐标
- 统一变换
- n 维向量使用 n+1
维向量表示
- 使用直线来表示点
- \((x,y)\) 使用 \((hx,hy,h),h\ne 0\) 来表示
- 标准齐次坐标:\(h=1\)
- 统一变换为 \(\vec{P'}=M\cdot\vec{P}\)
1. 平移变换
- translate
\[ M=T(t_x,t_y)=\begin{bmatrix}1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \]
2. 旋转变换
\[ M=R(\theta)=\begin{bmatrix}\cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
3. 尺度变换
\[ M=S(s_x,s_y)=\begin{bmatrix}s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
4. 复杂的变换
- 解构成基本变换
(1) 对任意点的旋转
平移参考点到原点
旋转
将参考点移回去
3 个矩阵变换
- 注意矩阵乘法不可交换,需要正确考虑顺序
两种模式
- 固定坐标系模式:先调用的先执行
- 活动坐标系模式:后调用的先执行(OpenGL)
- 变换结束之后更新的是坐标系
左乘 vs 右乘
左乘:行变换
\[ M\begin{pmatrix}x_1 \\ x_2 \\ x_3 \end{pmatrix} \]
- 右乘:列变换
\[ \begin{pmatrix}x_1, x_2, x_3 \end{pmatrix}M \]
(2) 对任意参考点的放缩
- 同理
5. 对称变换
- symmetric
(1) 关于 x 轴的对称变换
- \(y\rightarrow -y\)
\[ M=\begin{bmatrix}1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
(2) 关于 y 轴的对称变换
- \(x\rightarrow -x\)
\[ M=\begin{bmatrix}-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
(3) 关于任意轴的对称变换
- 解构
- 步骤
- 平移轴至过原点
- 绕原点旋转轴至与 x 轴或 y 轴重合
- 对称变换
- 旋转回去
- 平移回去
6. 错切变换
- shear
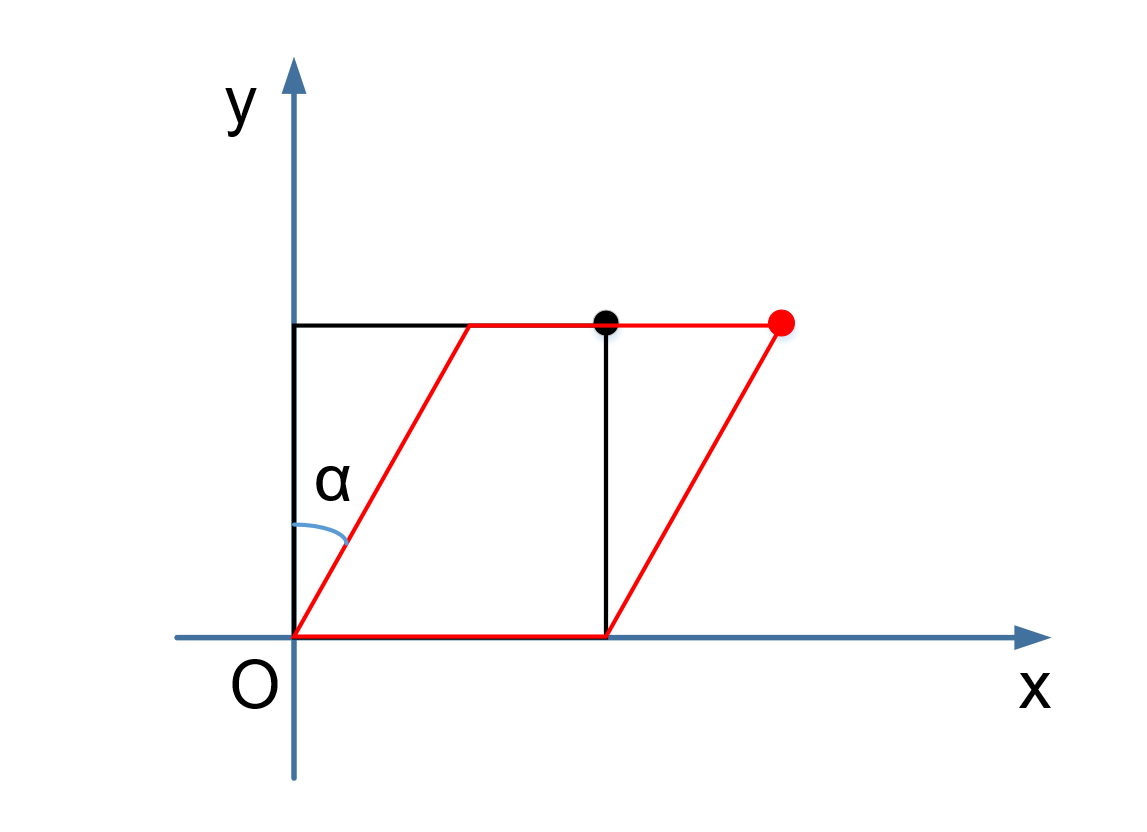
(1) 以 y 轴为依赖轴,y=0 为参考轴
- y 不变,x 错切
\[ M=\begin{bmatrix}1 & sh_x & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix},sh_x=\tan\alpha \]
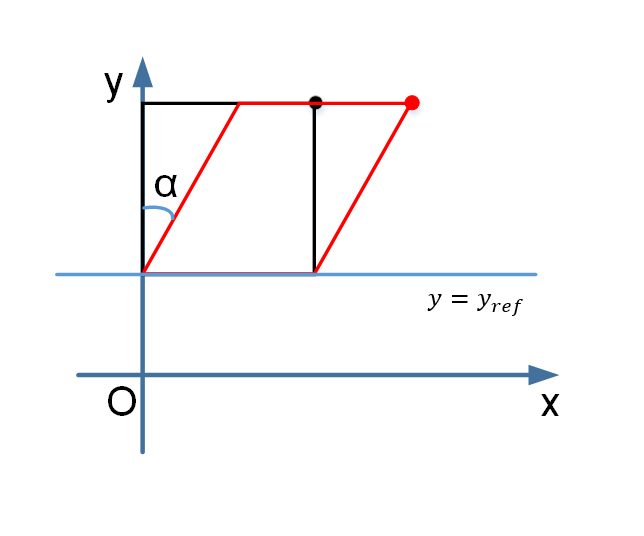
(2) 以 y 轴为依赖轴,\(y=y_{ref}\) 为参考轴
- 平移,错切(y=0),反平移
\[ M=\begin{bmatrix}1 & sh_x(1-y_{ref}) & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix},sh_x=\tan\alpha \]
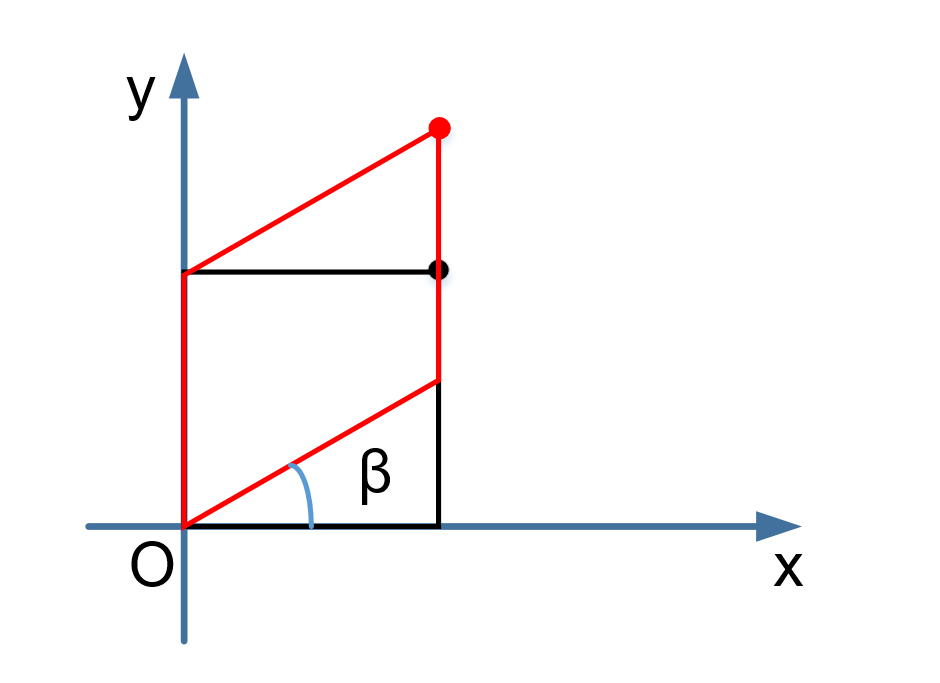
(3) 以 x 轴为依赖轴,x=0 为参考轴
- x 不变,y 错切
\[ M=\begin{bmatrix}1 & 0 & 0 \\ sh_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix},sh_x=\tan\beta \]
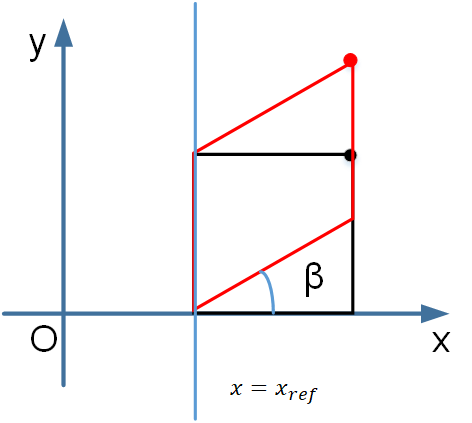
(4) 以 x 轴为依赖轴,\(x=x_{ref}\) 为参考轴
\[ M=\begin{bmatrix}1 & 0 & 0 \\ sh_y(1-x_{ref}) & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix},sh_x=\tan\beta \]
7. 仿射变换
- 以上提到的变换都是仿射变换
- Affine Transform
- 保持直线的平行性
- 正交投影属于仿射变换,透视投影不属于仿射变换
- 矩阵特征
\[ \begin{bmatrix}a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \]
二维图形的显示流程
- 世界坐标系(world coordinate)
- 或者称作用户坐标系(user coordinate)
- 局部坐标系(local coordinate)
- 屏幕坐标系(screen coordinate)
- 或者称作设备坐标系(device coordinate)
- 窗口 与 视区
- 窗口:在世界坐标系中指定的矩形区域,用来指定要显示的图形
- 视区:在设备坐标系上指定的矩形区域,用来指定窗口内的图形在屏幕上显示的大小及位置
三维几何变换
- 三维齐次坐标:\((x_h,y_h,z_h,h),h\ne 0\)
- 标准齐次坐标:\((x,y,z,1)\)
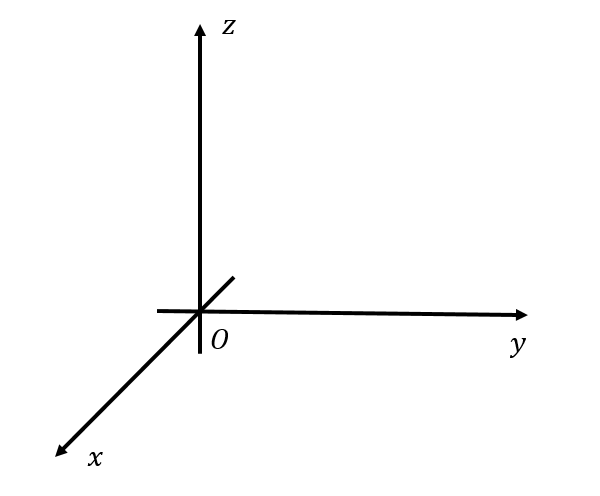
- 右手系:\(\vec{x} \times \vec{y} = \vec{z}\)
1. 平移 translate
\[ T(t_x,t_y,t_z)= \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
2. 尺度(放缩) scale
\[ S(s_x,s_y,s_z)= \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
3. 旋转 rotate
- 正方向:大拇指指向绕的轴的方向,四指的方向即为正方向
(1) 绕 x 轴
- x 不变
- 相当于在 yOz 平面旋转 \(\theta\)
- 划去 x 对应的列和行之后和二维相同
\[ R_x(\theta)= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
(2) 绕 y 轴
- y 不变
- 在 zOx 平面旋转 \(\theta\)
- 在 xOz 平面旋转 \(-\theta\)
\[ R_y(\theta)= \begin{bmatrix} \cos\theta & 0 & \sin\theta & 0\\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \]
(3) 绕 z 轴
- z 不变
- 绕 xOy 平面旋转 \(\theta\)
\[ R_z(\theta)= \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0\\ \sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
4. 错切 shear
- z 轴为依赖轴,z=0 平面为参考平面
\[ SH_z(sh_x,sh_y)= \begin{bmatrix} 1 & 0 & sh_x & 0 \\ 0 & 1 & sh_y & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
5. 对称变换
- 关于 z=0(xOy) 平面的对称变换
\[ SY_{xy}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
6. 仿射变换一般形式
\[ A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & a_{14} \\ 0 & 1 & 0 & a_{24} \\ 0 & 0 & 1 & a_{34} \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} a_{11} & a_{12} & a_{13} & 0 \\ a_{21} & a_{22} & a_{23} & 0 \\ a_{31} & a_{32} & a_{33} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = T\cdot M \]
- T 表示平移变换,M 表示其他变换
- 注意拆解顺序
7. 法向变换
- 点坐标:\((x,y,z,{\color{red}1})\)
- 点
- 法向坐标:\((x,y,z,{\color{red}0})\)
- 向量
- 验证:
- 点 - 点 = 向量
- 向量 + 向量 = 向量
- 点 + 向量 = 点
- 向量变换
- 取向量上两个不同点 \(x_1,x_2\),变换矩阵 \(A\)
- 原来的向量:\(x_2-x_1\)
- 新的向量:\(Ax_2-Ax_1\)
- 切向量:\(T\)
- 变化矩阵 \(M\)
- \(Mx_1-Mx_2=M(x_1-x_2)=M\cdot T\)
- 法向量:\(N\)
- 原始条件:\(N\cdot T=N^TT=0\)
- \(N'\cdot T'=(GN)\cdot(MT)=0\)
- 以上是向量乘法,转化为等价的矩阵乘法
- \((GN)\cdot (MT)=(GN)^T(MT)=N^TG^TMT=0\)
- \(\Rightarrow G^TM=I\)
- 即法向量的变换矩阵 \({\color{red}G=(M^{-1})^T}\)
- 当矩阵 \(M\) 为正交矩阵的时候,\(G=M\)